¿Alguna vez te has preguntado qué es tangente y cómo se aplica en la vida diaria? La tangente es un concepto fundamental en matemáticas, especialmente en geometría y trigonometría. Este término, que puede parecer complicado al principio, es en realidad bastante accesible cuando se desglosa. En este artículo, exploraremos en profundidad qué es tangente y su relevancia en varios campos, desde la física hasta la ingeniería.
La tangente se refiere comúnmente a la relación entre los lados de un triángulo rectángulo y se utiliza para describir la pendiente de una línea en un plano. A medida que avanzamos, definiremos la tangente en diferentes contextos y explicaremos cómo se puede calcular, así como su importancia en la resolución de problemas cotidianos. Prepárate para un viaje fascinante a través de las matemáticas y su aplicación práctica.
Además, veremos cómo la tangente se relaciona con otras funciones trigonométricas, como el seno y el coseno, y cómo estas se utilizan en diversas disciplinas. Desde la arquitectura hasta la navegación, la tangente es una herramienta esencial que permite a los profesionales resolver problemas complejos. Así que, sin más preámbulo, ¡comencemos a desentrañar el misterio de "que es tangente"!
¿Qué es la Tangente en Matemáticas?
La tangente es una función trigonométrica que se relaciona con la medida de ángulos en un triángulo rectángulo. Se define como el cociente entre el lado opuesto al ángulo y el lado adyacente. La fórmula matemática se expresa como:
tan(θ) = lado opuesto / lado adyacente
¿Cómo se Calcula la Tangente?
Para calcular la tangente de un ángulo, puedes usar una calculadora científica o aplicar la relación mencionada anteriormente en un triángulo. Aquí hay algunos pasos básicos para calcular la tangente:
- Identifica el ángulo θ que deseas calcular.
- Mide la longitud del lado opuesto al ángulo.
- Mide la longitud del lado adyacente al ángulo.
- Aplica la fórmula tan(θ) = lado opuesto / lado adyacente.
¿Dónde se Utiliza la Tangente?
La tangente tiene múltiples aplicaciones en la vida cotidiana, tales como:
- Ingeniería: En el diseño de estructuras y en cálculos de fuerzas.
- Navegación: Para calcular rumbos y distancias.
- Arquitectura: En el diseño de rampas y escaleras.
- Física: Para resolver problemas de movimiento y gravedad.
¿Qué es la Tangente en Geometría?
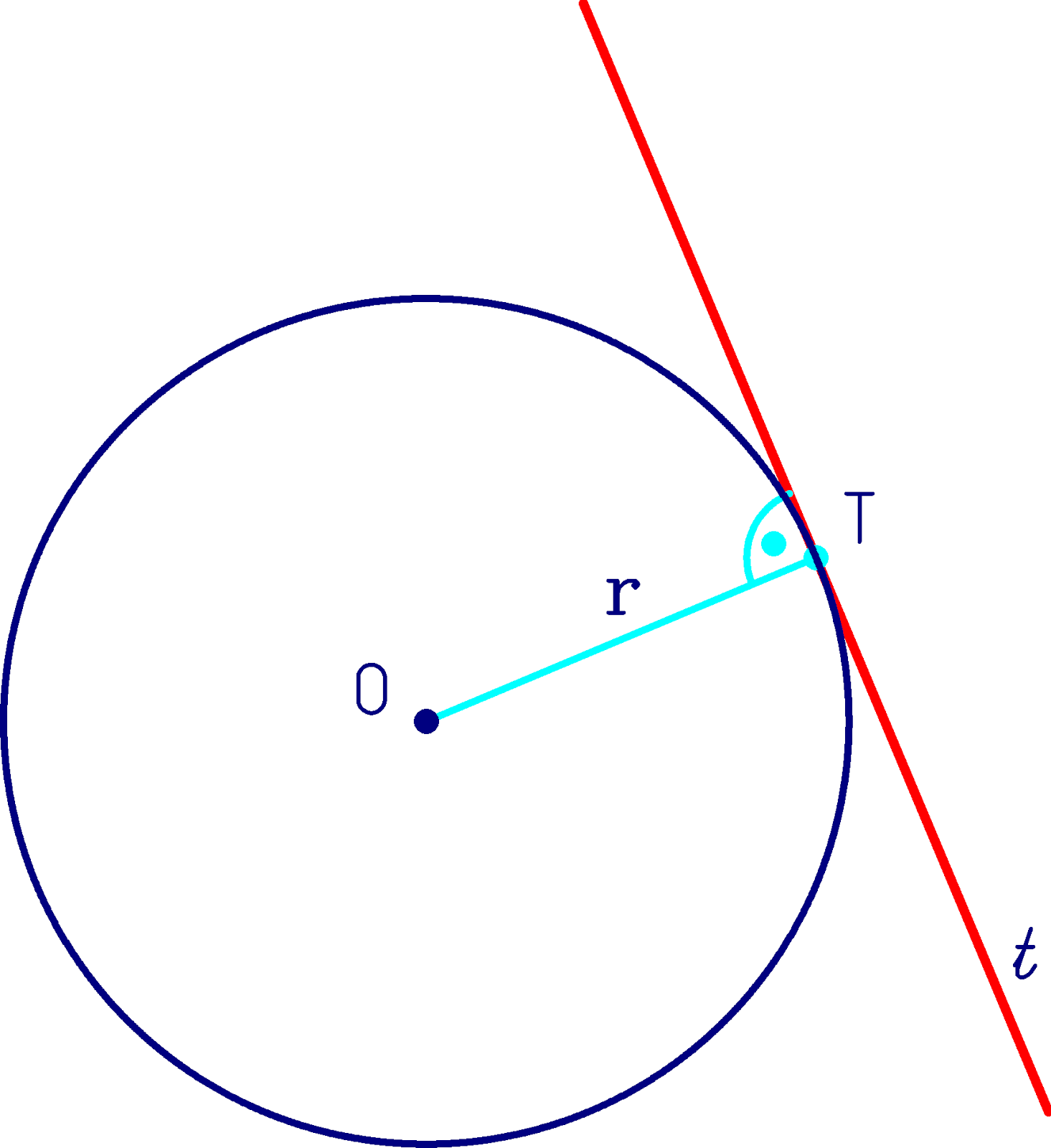
En geometría, la tangente también se refiere a la línea que toca una curva en un solo punto. Esta línea se utiliza para determinar la dirección de la curva en ese punto, lo que es crucial en el cálculo y la física. La tangente a una curva en un punto específico se puede calcular utilizando el concepto de derivadas en cálculo.
¿Cuál es la Diferencia entre Tangente y Otras Funciones Trigonométricas?
La tangente es una de las seis funciones trigonométricas básicas. A continuación, se presentan las diferencias clave entre la tangente y otras funciones trigonométricas:
| Función | Definición |
|---|---|
| Seno | Relación entre el lado opuesto y la hipotenusa. |
| Coseno | Relación entre el lado adyacente y la hipotenusa. |
| Secante | Recíproco del coseno. |
| Cosecante | Recíproco del seno. |
| cotangente | Recíproco de la tangente. |
| Tangente | Relación entre el lado opuesto y el lado adyacente. |
¿Por Qué es Importante Comprender la Tangente?
Comprender la tangente es crucial para el desarrollo de habilidades matemáticas y analíticas. Aquí algunas razones para estudiar la tangente:
- Facilita la resolución de problemas en campos técnicos y científicos.
- Permite comprender conceptos más avanzados en matemáticas, como el cálculo.
- Es esencial para aplicaciones prácticas en la vida diaria.
¿Cómo se Representa Gráficamente la Tangente?
La representación gráfica de la función tangente muestra cómo varía la tangente con respecto al ángulo. La gráfica es periódica y presenta asíntotas verticales donde la tangente no está definida. Esto ocurre cuando el ángulo es igual a (π/2 + nπ), donde n es un entero. La gráfica se asemeja a una serie de ondas que suben y bajan, lo que representa visualmente el comportamiento de la tangente.
¿Qué Relación Tiene la Tangente con el Cálculo?
En cálculo, la tangente se utiliza para analizar funciones y sus derivadas. La derivada de la función tangente se puede expresar como:
d/dx(tan(x)) = sec^2(x)
Esto significa que la tasa de cambio de la tangente es igual al cuadrado de la secante, lo que es fundamental en el estudio de la dinámica de las funciones.
¿Cómo se Aplica la Tangente en la Vida Diaria?
La tangente no solo se queda en el ámbito académico; tiene aplicaciones prácticas en diversas profesiones. Por ejemplo:
- Los arquitectos utilizan la tangente para calcular la inclinación de techos y rampas.
- Los ingenieros mecánicos aplican la tangente en el diseño de maquinaria.
- Los pilotos de avión utilizan la tangente para calcular ángulos de ascenso y descenso.
En conclusión, "que es tangente" es más que un simple término matemático; es una herramienta valiosa utilizada en diferentes disciplinas que afectan nuestra vida diaria. Desde la navegación hasta la ingeniería, la tangente nos ayuda a entender y resolver problemas complejos de manera efectiva. Así que la próxima vez que te encuentres con la tangente, recuerda su importancia y cómo se aplica en el mundo que nos rodea.
Billionaire Robert Smith's Wife: A Journey Through Love And Success
Discovering The Charm Of Abbott Elementary: A Deep Dive Into The Trailer For Season 1
Discovering The Culinary Delights Of Filipino Food In NYC